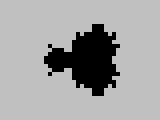
This is an essay I produced while an undergraduate, back in 1993. It's a bit long but was good fun to work on and write. I've made small changes to the text here and there, but nothing major. I have tidied up the formatting a bit. While preparing this web page, I was curious as to how a modern PC would do at the Turing simulation, and the results are given in the "Update" section.
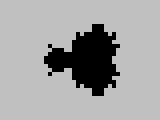
The Turing machine was introduced in Alan Turing's 1936 paper "On Computable Numbers, with an application to Entscheidungsproblem", and was proposed as a theoretical model to explore what could and could not be done by the computer, which was beginning to be developed at that time. It is based on a simplification down to the barest level of the actions of a human agent in carrying out an algorithm, using pen and paper, for performing some computational task.
The paper is modelled by an infinite strip of paper tape divided into square cells; if the tape were finite, there would always be some calculation which the machine could not perform simply because it ran out of tape, and this would hamper the theoretical development of the ideas. However, the rest of the machine is constructed in such a way that any calculation producing a result uses only a finite amount of the tape. Each cell is capable of having one symbol written on it from a finite set known as the machine's alphabet.
The pen is modelled by a mechanical read/write head which can "see" one cell of the tape at a time, and is capable of writing a new symbol to this cell. The actual task of executing an algorithm is performed by two actions which the machine is capable of, namely writing a new symbol on the cell currently under the head and moving the head to the left or right (or, equivalently, moving the tape to the right or left).
At any given time the machine is in one of a finite number of internal "states", perhaps representing the state of mind of the human agent modelled, numbered from zero upwards. The machine operates in a series of discrete steps, each imagined to take a given fixed length of time. At each step, its actions are determined by its current internal state and the symbol in the cell currently under its head. These decisions are given in the form of a "state table", which is fixed within the machine. Each row of the state table consists of two entries, the environment entry and the operation entry. The environment entry is an ordered pair; the first component is a state number and the second a symbol from the alphabet. The operation entry is an ordered triple; the first entry is a symbol, the second an element of the set {L, R, H} and the third a state number.
When switched on, the machine starts in state zero. Then, at each subsequent step, the machine searches in the state table for a row whose environment entry's first component is the same as the machine's internal state number and second component is the symbol on the cell under the head. It then replaces the symbol on that cell with the first component of the operation entry of that row, moves the head to the left or right as the second component is L or R, and enters the state given by the third component. If the second component of the operation entry is H, the machine halts. (In this case, of course, the third component is of no consequence.) The machine also halts if there is no row in the state table corresponding to its current environment, ie. matching its current state and symbol read. To avoid ambiguity, there must be no two rows in the state table with identical environment entries. The "length" of a state table is defined to be the largest state number appearing in an environment entry.
Mathematically, the whole Turing machine is coded by the state table, and so we can define a Turing machine to be its state table, ie. the set S of ordered pairs (environment, operation) forming the table.
As an example to illustrate the working of a Turing machine, consider a machine whose alphabet is {o, x} and whose state table is
| Environment | Operation | ||||
|---|---|---|---|---|---|
| State | Symbol | Symbol | Move | State | |
| 0 | o | x | L | 1 | |
| 0 | x | o | L | 2 | |
| 1 | o | x | R | 1 | |
| 1 | x | x | L | 2 | |
| 2 | x | x | L | 0 | |
acting on the tape
| ... | o | x | o | x | x | o | ... |
where the bold box represents the starting position of the head. The machine starts in state 0, and the symbol under the head is x; the operation entry in the table corresponding to the environment entry (0, x) is (o, L, 2), so the tape is altered to "...oxoxoo...", the machine moves left and enters state 2:
| ... | o | x | o | x | o | o | ... |
The environment entry now searched for is (2, x) which has corresponding operation entry (x, L, 0) so the tape is left unaltered, the machine moves left and enters state 0:
| ... | o | x | o | x | o | o | ... |
It is easily verified that the next two stages in the machine's operation are
| ... | o | x | x | x | o | o | ... | with the machine in state 1 |
followed by
| ... | o | x | x | x | o | o | ... | with the machine in state 2. |
There is, however, no entry in the state table with environment entry (2, o) and so the machine halts.
It is, of course, possible that such a machine will never halt; consider for example the following trivial (and contrived) state table, for a machine whose alphabet consists of the set {o, x}.
| Environment | Operation | ||||
|---|---|---|---|---|---|
| State | Symbol | Symbol | Move | State | |
| 0 | o | o | L | 0 | |
| 0 | x | x | L | 0 | |
Such a state table will cause the machine to move relentlessly leftwards down the tape, changing nothing. There are other less trivial circumstances which might cause the machine to never halt; division by repeated subtraction would not stop if the divisor were zero, for example. Study of the exact circumstances under which a Turing machine does and does not stop leads to the famous Halting Problem; it is not, however, our intention to study such things here. We shall be concerned with studying the implementation of useful operations on a Turing machine, which must necessarily halt.
The Turing machine is usually used to develop the idea of computability of functions from the natural numbers to the natural numbers and so is often seen as a purely theoretical device. However, in the remainder of this essay we will discuss how one might program a Turing machine to perform a real-world computational task.
The task chosen is that of plotting an image of the Mandelbrot set, a fractal beloved of many computer enthusiasts. The Mandelbrot set is based around the iteration
z0 = 0;
zn+1 = (zn)2 + c,
where c is a complex constant. We may view this process as a sequence of functions of c, by defining
f0(c) = 0;
fn+1(c) = fn(c)2 + c.
The Mandelbrot set M is then defined by
M = {c : |fn(c)| remains bounded as n tends to infinity}.
It can be proved that if |fn(c)| > 2 for some n and c, then |fn(c)| tends to infinity as n tends to infinity for that value of c. This forms the basis of an algorithm for plotting an approximation to M; to determine whether a particular point c of the complex plane lies inside M, compute f0(c), f1(c) and so on. If at any time |fn(c)| exceeds 2, then the point does not lie in M. If we have computed a large number of iterations and |fn(c)| has not exceeded 2, then we guess that it never will and conclude that c is a member of M. By "a large number" we mean typically values of the order of hundreds, although for more accurate images of smaller sections of the plane values of several tens of thousands are used. Obviously this algorithm will sometimes wrongly conclude that c lies in M; the value of |fn(c)| may go outside a circle of radius 2 on the iteration after we have given up; but in practice this method yields acceptable images.
Extending this algorithm to one which will plot an approximation to M involves setting up a discrete grid of points to be checked for membership of M. The actual image is then generated by colouring a small rectangle, on paper or a computer screen, according to whether the corresponding point in the grid was inside M.
Preliminary experiments show that a pleasing image is contained in the rectangle
-2.5 < Re(c) < 1.5,
-1.5 < Im(c) < 1.5;
we will use a grid of 40 points in the real direction by 30 in the imaginary direction covering this area. Usually the grid is several hundred points on each side, but we will limit ourselves to this coarse grid in order to reduce the computation time. Also, a simple induction gives that fn(c*) = (fn(c))*, and since |z| = |z*|, we deduce that M is symmetrical about the imaginary axis. This cuts the computation required in half as we need now only test those points of the grid which lie below the imaginary axis. Our grid is therefore 40 by 15, and elementary calculations show that the bottom left sample should be at -2.45 - 1.45i with subsequent samples being on a 0.1 by 0.1 grid, giving the top right sample to be at 1.45 - 0.05i. Preliminary experiments show that an acceptable image is produced by taking the "large number" for the iteration counter limit to be 15; substantially smaller than is usual.
In order for the Turing machine to perform any useful function, protocols must be established giving how we are to provide the machine with its input, and how we are to interpret the symbols left on the tape when the machine halts. We must first decide on the actual symbols to use, ie. the alphabet of the machine. Since we shall be studying a computational aspect of the machine, we shall use the set {0, 1} as our alphabet, basing our machine on the binary system, in common with all real-world electronic computers since ENIAC, the first and only base ten electronic computer built.
Turing machines were originally designed to evaluate natural-number-valued functions of tuples of natural numbers, and so we first look at methods of representing an arbitrary-length tuple of natural numbers for the input to the machine and a way of interpreting the symbols left on the tape at the conclusion of the machine's run as a natural number.
The protocol suggested by Cutland [p56, Computability, An introduction to recursive function theory] is as follows (his alphabet consists of the set {B, 0, 1}, but the symbol 0 is not used in the protocol, so the system could trivially be adapted to the alphabet {0, 1}). To prepare the input tape, we first consider how to represent a single natural number x. This is done by writing (x + 1) 1s contiguously on the tape; the remainder of the cells of the tape contain Bs. (x + 1) 1s are used to distinguish a tape representing zero from a blank tape. An n-tuple of natural numbers is then represented by n such numbers, each separated from its neighbours by a cell containing "B". For example,
...BBBBB111111B111111111111111B11111B1BBBBBBBBBB...
would represent the ordered 4-tuple (5, 14, 4, 0). When the machine halts, the output, ie. the value of the function it has computed, is taken to be the total number of 1s on the tape. For example
...BBBBBBBBBB1BB11B11111B111BBBBBBB111BBBBBB11BB...
would represent the output 16.
For practical purposes, however, this method has two rather major flaws. Firstly, to give the machine the input triple (163612, 22763, 9382661) would require a very large amount of tape. This is not, of course, a problem theoretically, since we have an infinite supply of it and we are not concerned with how long the machine takes to produce its output. However we require a rather more compact method. The second flaw is that, even for purely theoretical purposes, it is very useful to be able to take the output of one program or function as the input to another, and the output tape given as an example above does not represent a valid input tape as there are several Bs between some of the strings of 1s. This would seriously hamper both the theoretical and practical development of Turing machines.
The next obvious method to consider, given our alphabet, is the binary system of numbering. The machine's head would start off at the right hand (i.e., least significant) end of a binary number, with all tape cells to the right of the head filled with 0s. For example, the tape
| ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |
where the arrow gives the starting position of the head, would represent the input number 10101100, or 172 in decimal. The output would be interpreted in exactly the same way, with anything to the right of the head being ignored.
When we try to represent, for example, an ordered pair of natural numbers by this method, however, a large problem becomes apparent. There is no way of delimiting the two numbers, ie. deciding where the first number ends and the second begins. For example, the tape
| ... | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |
could represent the pair (1464, 23128), the pair (23435, 600), or many others.
One way of solving this problem is to agree that each number is only a certain fixed number, say n, of binary digits ("bits") long. From a theoretical point of view this is no solution at all, because we then have no way of representing any natural number greater than 2n - 1. From a practical point of view, however, this is less important because we can use various methods to represent numbers other than the natural numbers 0 to 2n - 1. This is, of course, done in real-world computers, which typically approximate real numbers by means of 64-bit binary numbers.
Closer inspection of the algorithm which our machine will be executing shows that there are relatively few numbers which must be kept track of, namely, the current value of fn(c), the number c itself, the iteration count n, and a few other counters for keeping track of where the computation is on the grid of points.
Therefore, it would seem a good idea to provide, by means of a suitable Turing machine state table and initial tape, a number of "registers", each of which is capable of holding (an approximation to) a real number or, alternatively, an integer. Complex numbers can then be represented by pairing two such registers and manipulating them appropriately.
These registers will be used to determine which points of the grid are in M, and another section of the tape will be used to hold the results, i.e., for each point in the grid, a coding of whether it lies in the set.
To be able to represent a real number, which is an infinite object, in a finite number of bits, we will employ a method known as fixed-point binary representation. This is a binary analogue of writing a number with a fixed number of decimal places: a number x is stored as the integer nearest to ax, where a is some large constant (typical values are of the order of millions). Operations are made easier if the value chosen for a is a power of the radix of the number system used, i.e., a power of two in the binary system.
To store the negative integers which will arise when storing a negative real number by this method, we will use the technique known as "two's complement". Here, if the binary number has k bits, the most significant bit is used as a "sign bit", ie. the bit in that position has a value of -2k - 1 instead of 2k - 1. Thus the range of integers which can be stored is [-2k - 1, 2k - 1 - 1]. When adding two k-bit numbers together, only the least significant k bits of the result are taken. This can cause problems with overflow, i.e., losing the most significant bits of the result; however no problems arise if no attempt is made to store an integer outside the permissible range given above.
By noting that a(x + y) = ax + ay, we see that addition can be
accomplished by simply adding the integer representations, and
since
a(xy) = (ax)(ay)/a,
multiplication is accomplished by multiplying the
representations and then dividing the result by a; if a is 2
A k-bit binary number with a taken to be 2n can therefore store real numbers in the range [-2k - n - 1, 2k - n - 1) with an accuracy of n bits after the binary point, i.e., roughly (n log 2/log 10) decimal places. Preliminary experiments suggest that taking k as 20 and n as 15, giving a range of [-16, 16) with about four decimal places' accuracy, produces reasonable results, and so the majority of the registers will be 20 bits long, with arithmetic coded appropriately for 15 bits after the point. For the multiplication routine, however, since two 20-bit numbers multiply to give a 40-bit number, we will require some 40-bit registers.
We must now deal with the problem of how these (mostly) 20-bit registers are to be stored as strings of 0s and 1s on the Turing machine's tape. The obvious solution, that of simply writing each of the 20 bits of each register on the tape, would make the implementation of arithmetic operations very difficult; addition, for example, is achieved by adding each bit of the two numbers from least to most significant in turn, keeping track of the "carry" between bits. If there is no way for the machine to mark its position in the register, then there is no immediately apparent way, as the machine has no internal counters besides its state number, to avoid having to repeat the basic adding logic 20 times to add two registers. Therefore, we will use the following method to store the registers.
Suppose we wish to store the 20-bit integer b19b18...b1b0. This will be done by writing the sequence
| ... | 1 | 0 | b19 | 0 | 1 | 0 | b18 | 0 | 1 | 0 | ... | 0 | 1 | 0 | b1 | 0 | 1 | 0 | b0 | 0 | 1 | ... |
on the tape. This seemingly verbose method of storage allows the machine to easily mark its position within a register during an operation. Note that nowhere in this section of tape do two 1s occur consecutively. Therefore, altering a 0 in one of the inter-bit 010 delimiters to a 1 will produce the unique marking of two (or maybe three) consecutive 1s, which the machine can easily search for, as we will see below. Which one is altered will depend on the direction from which the machine will be searching. If the machine will be coming from the right, the delimiter will become 110, if the left, 011. This is to avoid confusions when the adjacent bits of the register are 1s.
By butting together several registers stored in this manner, a tape such as
| ... | 1 | 0 | b1,19 | 0 | 1 | 0 | ... | 0 | 1 | 0 | b1,0 | 0 | 1 | 1 | 0 | b2,19 | 0 | 1 | 0 | ... | 0 | 1 | 0 | b2,0 | 0 | 1 | 1 | 0 | b3,19 | ... |
will result. Here, bi,j denotes the jth bit of register i. Thus bits are delimited by the sequence 010 and registers by the sequence 0110, containing two consecutive 1s, which as mentioned above, is easy to search for.
The first register will be preceded by the sequence 011, thereby producing a string of three consective 1s, demarcating the section of the tape containing the registers (that to the right) from the section which will eventually contain the output (that to the left).
Having decided on the format of the section of the tape which will store the registers used, we must find a protocol for the section of tape to the left of the registers/output 01110 delimiter. First consider what it is the machine will output; a verdict of "in M" or "not in M" for each of the points in the grid. Suppose we represent "in M" by 0, and "not in M" by 1. Then provided we agree in which order the points should be tested, the problem is reduced to representing a string of 0s and 1s on the tape. Note that the string will be encoded on the tape in such a fashion to require the tape to be read from right to left, ie. from the registers/output delimiter leftwards. The obvious solution, writing 0 on the tape for a 0, and 1 for a 1, produces the same difficulties as trying to represent two binary numbers on a tape -- there is no way of telling where we have got to. For example, the tape
| ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | ... |
where the bold box marks the start of the delimiter, could represent the string 1, 0, 1, 1, 0, 1 (reading from right to left), or the string 1, 0, 1, 1, 0, 1, 0, 0, 0, and so on.
We could use the same method as for the registers, ie. delimiting each bit by the sequence 010; however in this case a more concise coding will suffice. We can code each digit as the number of 1s between pairs of 0s, terminating with two 1s; for example 110101 would code as 1101001001010 (recall the tape reads from right to left), and 11010001010101000 would represent 001111001. With this method, to append another bit to the string, we can search leftwards to find the two 1s, remove them, write the new bit and replace the two 1s. This will be made precise below.
Most algorithms are presented as a list of instructions to be carried out, either by a human agent or by a computer of some sort. The Turing machine, on the other hand, does not operate in this fashion; rather its "instructions" are given in the state table. To implement an algorithm presented in the "usual" fashion, for example the Mandelbrot plotting algorithm, on a Turing machine, therefore, requires that we turn a list of instructions into a state table for the machine.
Supposing for the moment that we have coded each individual instruction of the algorithm into a state table, we consider the problem of how to ensure that execution proceeds from one to the next, with a couple of exceptions which we will discuss below. To do this, we require the notion of a state table in "standard form".
Let the length of a given state table be N. Then the state table is in standard form if there is no operation entry with its second component 0 and the only state numbers appearing in the third component of an operation entry are 0, 1, ..., N, N+1. A Turing machine with a state table in this standard form will therefore only halt (if at all) when it tries to enter state N+1, for which there is no entry in the table.
We claim that for every Turing machine state table, there is an equivalent table in standard form. By "equivalent" we mean that the effect of the machine on any tape is the same as that of the original machine.
Let a state table be given, and suppose its length is K. Then for each entry in the given state table, produce a new one by mapping
| Environment | Operation | ||||
|---|---|---|---|---|---|
| State | Symbol | Symbol | Move | State | |
| k | r | w | m | s | |
to
| Environment | Operation | ||||
|---|---|---|---|---|---|
| State | Symbol | Symbol | Move | State | |
| k | r | w | m' | s' | |
where
| m' = | m, | if m != H; |
| R, | if m = H; | |
| s' = | s, | if s <= K and m != H; |
| K + 2, | if s > K and m != H; | |
| K + 1, | if m = H. |
Also add two new state table lines:
| Environment | Operation | ||||
|---|---|---|---|---|---|
| State | Symbol | Symbol | Move | State | |
| K + 1 | 0 | 0 | L | K + 2 | |
| K + 1 | 1 | 1 | L | K + 2 | |
Then it is easy to see that the only difference between the two state tables is in the method of halting, so the effect on any tape is the same. The new lines ensure that the final position of the head is the same as in the original state table. In what follows, we shall, where possible, write the state tables in standard form in the first place and so avoid having to remap them as above.
We also need to introduce the concept of "relocation" of a state table. Given a state table S and a non-negative integer R, we can produce a new state table S[R] by mapping each entry
| Environment | Operation | ||||
|---|---|---|---|---|---|
| State | Symbol | Symbol | Move | State | |
| k | r | w | m | s | |
to
| Environment | Operation | ||||
|---|---|---|---|---|---|
| State | Symbol | Symbol | Move | State | |
| k + R | r | w | m | s + R | |
The state table S[R] thus produced is said to be the result of relocating S with an offset of R.
The benefit of introducing these two definitions is that we are now in a position to arrange what is in effect the consecutive operation of two separate Turing machines on a tape. Let S and T be two Turing state tables in standard form, and let R be the length of S. Then it is easy to see that the state table (S union T[R]) will give a Turing machine which first performs on the tape the operations coded by S and then those coded by T. Of course, if S does not halt then T will never be performed, but as mentioned above, this will not occur with the state tables relevant to the Mandelbrot set problem. It is clear how we may extend this process to produce the consecutive operation of any number of state tables.
The exceptions to the requirement that each algorithm instruction should be in standard form are in coding instructions such as "go to step 12" and "if the symbol under the head is 0 then go to step 9". As noted above, a sequence of state tables in standard form concatenated as described will always execute in that sequence and no other. We would thus be restricted to those algorithms which make no decisions; a severe limitation.
The "goto" type of instruction can be coded as follows. Suppose an algorithm consists of instructions I1, I2, ..., In, and that these instructions have been coded as state tables (in standard form, with the exception of the two types of instruction mentioned above) as S1, S2, ..., Sn. Let the length of these state tables be L1, L2, ..., Ln respectively. Let M1 = 0 and Mk + 1 = Mk + Lk for 2 <= k < n, so that when relocated, the state table for instruction i, Si, starts with state Mi, and the concatenated state table is given by UNIONi(Si[Mi]). Suppose instruction i is "go to instruction j", where 1 <= i, j <= n. Then we may produce Si (necessarily not in standard form) thus:
| Environment | Operation | ||||
|---|---|---|---|---|---|
| State | Symbol | Symbol | Move | State | |
| 0 | 0 | 0 | R | 1 | |
| 0 | 1 | 1 | R | 1 | |
| 1 | 0 | 0 | L | Mj - Mi | |
| 1 | 1 | 1 | L | Mj - Mi | |
since when instruction i is to be executed, the machine will enter state Mi, ie. state 0 in the above table since the table shows Si before its relocation. The symbol will not be altered, the head will move one cell to the right, and the machine will enter state 1 (as written in the above table). Again the symbol will not be altered, the head will move left to return to its original position, and the machine will enter state Mj - Mi, which after relocation by Mi will become state Mj, i.e., the start of Sj as required.
The instructions which implement decisions, ie. those of the form "if the symbol under the head is 0 then go to step 7" can be coded in a similar way, but with the operation entries differing for environment entries with different symbol components. Again, such state tables will necessarily not be in standard form. For example, in the set-up described in the discussion on "goto" instructions, suppose that instruction i is "if the symbol under the head is 0 then go to step j; if it is 1 then go to step k". This can be coded thus:
| Environment | Operation | ||||
|---|---|---|---|---|---|
| State | Symbol | Symbol | Move | State | |
| 0 | 0 | 0 | R | 1 | |
| 0 | 1 | 1 | R | 2 | |
| 1 | 0 | 0 | L | Mj - Mi | |
| 1 | 1 | 1 | L | Mj - Mi | |
| 2 | 0 | 0 | L | Mk - Mi | |
| 2 | 1 | 1 | L | Mk - Mi | |
It is easy to see that this produces the required effect.
Note that in both of the examples given above, the head is left in the same position after the execution of the instruction as it was before. If the head position were to be altered, the side-effects of this on the algorithm would have to be taken into consideration, and it is usually easier not to have to do this. However, in some instances it saves state table entries if a head movement can be incorporated into the decision instruction, and this will be done, when useful, in coding the arithmetic instructions which follow.
Algorithms such as
1. Move right 2. Write a 0 3. Move left twice 4. Write a 1
contain instructions which are simple enough to be coded directly as Turing state tables; however an instruction such as "move the contents of register 7 into register 3" is less straightforward. Such instructions must be broken down into much simpler steps before they can be coded as state tables. Therefore, we now briefly look at some of the very simple sub-operations which will be used to build the more complex arithmetic instructions.
To avoid having to write out a table each time a coding is presented, simpler state tables will be given in the form
i1 r1 w1 m1 j1; i2 r2 w2 m2 j2; ...
where the environment entry is (i, r) and the operation entry (w, m, j).
The operation "move left" can be coded "0 0 0 L 1; 0 1 1 L 1" and similarly for "move right". "Write 0" can be coded "0 0 0 L 1; 0 1 0 L 1; 1 0 0 R 2; 1 1 1 R 2", making sure that the head position is not altered, and similarly for "write 1".
Another type of instruction is that of the type "move left until 3 consecutive 1s are found"; this example can be coded as
| Move left until 3 consecutive 1s are found | |||||
|---|---|---|---|---|---|
| Environment | Operation | ||||
| State | Symbol | Symbol | Move | State | |
| 0 | 0 | 0 | L | 0 | |
| 0 | 1 | 1 | L | 1 | |
| 1 | 0 | 0 | L | 0 | |
| 1 | 1 | 1 | L | 2 | |
| 2 | 0 | 0 | L | 0 | |
| 2 | 1 | 1 | L | 3 | |
where the head is then left just to the left of the first run of 3 consecutive 1s encountered. The example can easily be adapted to code instructions such as "move right until 4 consecutive 0s are found". The instruction "move left (right) until n consecutive bs are found" will be written "Lto n b" ("Rto n b") for brevity.
We must now consider how the instructions needed to perform arithmetic on the registers stored on the tape can be coded. By the results of the preceding section, we can see that it will be enough to write an algorithm using just the instructions "move left/right", "write 0/1", "Rto n b", "Lto n b" and those of the "go to" and "if ... then ..." type. Movement instructions will be abbreviated to "Ln" for "move left n times" and similarly for "Rn", with an absent n taken to be 1. When it is necessary to include an explicit state table in the coding, this will be written in the "i1 r1 w1 m1 j1; i2 r2 w2 m2 j2; ..." form described above. It will often not be necessary to give each instruction of an algorithm a step number, and so labels will be used to mark those instructions to which it will be necessary to jump. These labels will be of the form ":label name:", and when one appears as the state number in an operation entry of a table, it is understood that this represents the state number (after relocation) of the start of the instruction immediately after the label.
We need to establish a convention for determining where the head will be at the start and end of each instruction executed. Fairly arbitrarily, we take this position to be over the first 1 of the 01110 registers/output delimiter. This will be the position of the head when the machine first starts, and we will write each operation in such a way that the head is left in this position at the completion of the operation.
We will often need to work on a specific register, and so we will write the following sequence as "FindReg i"
FindReg i R3 Rto 2 1 ... (i times) Rto 2 1 L2
This will position the head over the first 1 of the delimiter which separates register i from register i + 1, i.e., at the least significant end of register i. Similarly, the following sequence will be written "FindStart"
FindStart Lto 3 1 R
This positions the head over the first 1 of the 01110 registers/output delimiter, i.e., the agreed "home" position of the head, provided that the head was to the right of the delimiter. This will, of course, be the case most of the time, when the machine is working with the registers.
The first operation required is to move the contents of one register into another. This will be required in transferring numbers to temporary working registers in more complex routines later on. It will also serve to introduce the method of working on registers one bit at a time, with the machine marking its position as it proceeds.
We will first code a "move" instruction for transferring the contents of a register to another of the same size. The instruction to move the contents of register j into register i (losing the old value of register i) will be written "Mov i j". We first present the algorithm, then explain its operation. It is necessary to split the operation into the cases i > j and i < j; the following algorithm is for the case i < j. Comments are given to the right of the instructions.
Mov i j for i < j FindReg i Move to least significant end L5 Move to first 0 of 010 Write 1 Change to a 1 R Rto 2 1 ... (i-j+1 times) Find just past lsb of register j Rto 2 1 L4 Move to bit :L0: "0 0 0 L 1; 0 1 1 L :L2:" Read bit and move left -- henceforth "move 0" Write 1 Leave 011 marker in register j L2 Is this the last bit ? "0 0 0 L 1; 0 1 1 R :L3:" If 0, no -- left and carry on; if 1, yes Lto 2 1 ... (i-j+1 times) Find marker left in register i Lto 2 1 R4 Move to the actual bit Write 0 and write the bit read from register j :L1: finished duplication according to bit now L3 Move to first 1 of 110 marker Write 0 Restore to 010 delimiter L4 Move to first 0 of next most sig. 010 delimiter Write 1 Leave 110 marker R Rto 2 1 ... (i-j+1 times) Find 011 marker left in register j Rto 2 1 L Back up to second 1 in 011 Write 0 and restore to 010 delimiter L3 Move to next bit to transfer Goto :L0: and loop round until all bits copied :L2: Henceforth "move 1" Write 1 Leave 011 marker in register j L2 Is this the last bit ? "0 0 0 L 1; 0 1 1 R :L4:" If 0, no -- left and carry on; if 1, yes Lto 2 1 ... (i-j+1 times) Find marker left in register i Lto 2 1 R4 Move to the actual bit Write 1 and write the bit read from register j Goto :L1: return to common code :L3: we have read the last bit which was a 0 R Move to the 1 written as a marker Write 0 and remove it L Lto 2 1 ... (i-j+1 times) Find most sig. end of register i Lto 2 1 R4 Move to the actual bit, Write 0 write the bit read from register j Goto :L5: and jump to common finishing code :L4: we have read the last bit which was a 1 R Move to the 1 written as a marker Write 0 and remove it L Lto 2 1 ... (i-j+1 times) Find most sig. end of register i Lto 2 1 R4 Move to the actual bit, Write 1 write the bit read from register j :L5: FindStart Leave head in its "home" position
The first step, up to :L0:, is to set up the register i with a marker to indicate where the first bit read from register j is to be written. This is achieved by changing the 010 to the left of the destination bit to 110. This can be searched for from the right by searching for two consecutive 1s in the midst of the register. The head then moves to the least significant end of register j, then backs up to be left over the first bit to be moved.
The state table at :L0: then reads the bit under the head and jumps to one of two different places in the state table depending on the bit read. This illustrates an important point, namely that anything that we wish the machine to "remember" as it moves backwards and forwards along the tape can only be stored as its internal state number. Therefore, to remember the value of the bit read, we must duplicate that section of the table between reading and writing the bit, with one copy being, in effect, "moving a 0", and the other "moving a 1".
After the bit has been read, a marker is left in the source register, register j; the delimiter to the left of the bit just read is now 011 instead of the usual 010, except if the bit just read was the most significant, in which case the register delimiter will now be 0111 instead of 0110. This is tested for, and if it was the last bit, execution jumps to the "finishing" section of code from :L3: onwards. If not, the head moves left until it finds the marker left in the middle of register i, the head is moved right to the actual destination bit, and the bit read from register j is then written. At this point the duplication of the state table mentioned above ceases, and from :L1: onwards the code is executed whether the bit read from register j was 0 or 1. This code moves the marker to the next bit left and then the head returns to the marker left in the source register and backs up to the next bit to read, at which point the situation is the same as when :L0: was first reached and therefore the code loops round to repeat the bit-moving operation.
When the last bit is detected, the register delimiter is restored to 0110, the head moves to the most significant end of register i and the bit is written. The head is then returned to its home position at the 01110 registers/output delimiter. Note that there is no need to erase the marker left in the destination register as when it was left, a 1 will have been written over the first 1 of the register 0110 delimiter (since the registers have the same number of bits).
If i > j, the algorithm differs only in the movement (to move from source to destination the head moves to the right and vice versa) and in the markers left (the source marker is now a 110 to the left of the bit just read, and the destination marker is now a 011 to the left of the bit to be written to). The full algorithm is as follows.
Mov i j for i > j FindReg i Find least significant end of register i L3 Move to second 0 of 010 delimiter Write 1 Change it to a 1 to give a marker L Lto 2 1 ... (i-j times) Find least significant end of register j Lto 2 1 L and move to the actual bit :L0: "0 0 0 L 1; 0 1 1 L :L2:" Read the bit and move left -- henceforth "move 0" L2 Move to first 0 of 010 delimiter Write 1 Change it to a 1 to give a marker R Rto 2 1 ... (i-j times) Find most significant end of register i Rto 2 1 "0 0 0 R 1; 0 1 1 R :L3:" Check whether this is the last bit to move Rto 2 1 No it isn't -- move to just past marker Write 0 and write the bit read L Move to second 1 of 011 marker :L1: duplication for bit read finished here Write 0 Restore delimiter to 010 L4 Move to next delimiter Write 1 and leave marker L Lto 2 1 ... (i-j+1 times) Find marker left in register j Lto 2 1 R Move to first 1 of 110 marker Write 0 and restore it to 010 delimiter L Move head to next bit to transfer Goto :L0: and loop round :L2: Henceforth "move 1" L2 Move to first 0 of 010 delimiter Write 1 Change it to a 1 to give a marker R Rto 2 1 ... (i-j times) Find most significant end of register i Rto 2 1 "0 0 0 R 1; 0 1 1 R :L4:" Check whether this is the last bit to move Rto 2 1 No it isn't -- move to just past marker Write 1 and write the bit read L Move to second 1 of 011 marker Goto :L1: and return to common code :L3: Write 0 Write the last bit which was a 0 Goto :L5: and jump to common "finishing" code :L4: Write 1 Write the last bit which was a 1 :L5: L Move to third 1 of 0111 reg. delimiter Write 0 and restore it to 0110 L FindStart Return head to its home position
The principle behind the operation of the algorithm is the same as in the case i < j -- read each bit one at a time, then move it to the destination register. The method of leaving markers in the registers differs slightly, as does the method of detecting when the last bit has been reached. We therefore leave the comments as the explanation of this code.
In the multiplication routine we will require "move" instructions which do not require the source and destination registers to be of the same size; multiplying two 20-bit numbers gives a 40-bit result, so we will need a "MovE" instruction which will move and extend a shorter register into a longer one, ie. copy the source register into the low-order bits of the destination, then copy the top bit of the source into the remaining, high order, bits of the destination. The top bit, rather than zero, is used in order to preserve the sign of the number. Also, we then need a "MovD" instruction which will move and de-extend a longer register into a shorter one. The low order bits are copied across, and the high-order bits of the source register are then ignored. Note that this could produce problems as we are potentially losing half of the information in a register, but as long as the number held in the source register can actually be represented in the destination, then no errors will occur.
The algorithms are similar to those presented above for the simple "Move" between same-sized registers; there is additional code to replicate the top bit in the "MovE" routine, and the method of detecting when the end has been reached differs slightly. They are given in Appendix A as they are too long to present in full here.
In the Mandelbrot iteration, z0 is (complex) zero, and so we require an instruction which will set a register to zero. Again, we present the algorithm and then explain its operation. The following instruction, written "Clr i", will zero register i.
Clr i FindReg i L "0 0 0 L 1; 0 1 1 R 3" "0 0 0 L 1; 0 1 0 L 1" "0 0 0 L -3; 0 1 1 L -3" FindStart
Here some of the state tables given use state number in the operation field which are outside the range defined by that table. This presents no difficulties as the numbers will give the correct results when the tables are relocated. Essentially the algorithm finds the start of the register, then moves leftwards, writing 0 in every bit of the register from the least to most significant end. It has reached the end of the register when the delimiter is 0110 instead of 010; this is detected in the third line of the algorithm.
When squaring a complex number, the imaginary part of the result is twice the product of the real and imaginary parts of the original complex number. In the binary system, multiplication by a power of two is easily and quickly achieved by shifting the number to the left, exactly as multiplying by a power of ten can be achieved in the decimal system. Also, as mentioned above in the discussion about real number representation, division by the large integer a = 2n can be achieved by shifting the number right n places.
In the case of the left shift of a k-bit number, the operation replaces bk-1 with bk-2, bk-2 with bk-3, and so on down to replacing b1 with b0. b0 is then set to 0. However, in the case of the right shift, the "empty" top bit bk-1 is preserved in order that sign overflows should not occur. For example, for a five-bit number, 11101 represents -5; shifting 11100 right preserving the top bit gives 11110, ie. -2 which is -5 divided by 2 (and truncated). If the top bit were zeroed, the result would be 01110, i.e., 14, the wrong result. (These protocols produce "arithmetic" shifts; the corresponding "logical" shifts both fill the empty bit with a 0. Logical shifts will not be used in the problem under discussion.)
We first present the algorithm for shifting a register left, as it is slightly the simpler of the two.
Shift register i left FindReg i L "0 0 0 L 1; 0 1 1 R 7" "0 0 0 L 1; 0 1 0 L 5" "0 0 0 L -3; 0 1 1 L -3" L "0 0 0 L 1; 0 1 1 R 3" "0 0 1 L -3; 0 1 1 L 1" "0 0 0 L -3; 0 1 1 L -3" FindStart
The four rows after the initial FindReg are essentially "carrying a 0", and the four rows after that "carrying a 1". The algorithm is therefore entered at the first four, to fill the empty bit with a 0. The third line of each group of four reads the bit under the head, writes the previously read bit and then jumps to the appropriate section of the algorithm. Again, the last bit is detected by the presence of a 0110 delimiter.
To shift a register right, we need, of course, to start at the most significant end, and so we introduce the instruction "FindSReg" for "find the significant end of register". "FindSReg i" will stand for the sequence of instructions
FindSReg i R3 Rto 2 1 ... (i-1 times) Rto 2 1 L2
which positions the head on the first 1 of the 0110 delimiter at the right hand, i.e., significant, end of register i. When i = 1 this gives "FindSReg 1" to be "R3, L2", ie. just "R", leaving the head over the second 1 of the 01110 registers/output delimiter, the correct position relative to the actual bits of the register.
Thus the algorithm to arithmetically shift register i right can be written
Arithmetic shift register i right FindSReg i R2 "0 0 0 R 4; 0 1 1 R 8" R "0 0 0 R 1; 0 1 1 L 7" "0 0 0 R 1; 0 1 0 R 5" "0 0 0 R -3; 0 1 1 R -3" R "0 0 0 R 1; 0 1 1 L 3" "0 0 1 R -3; 0 1 1 R 1" "0 0 0 R -3; 0 1 1 R -3" FindStart
The bulk of this algorithm is the same as that for shifting a register left, except that, of course, the head proceeds rightwards. The first three lines read the top bit and then jump to the appropriate section of the main algorithm. The last bit is detected in the same way as before.
To add two complex numbers together, as will be required in the Mandelbrot iteration, it is obviously sufficient to be able to add two real numbers (represented in fixed point format). This is achieved in binary much as in decimal, working from the least significant to the most significant bit, "carrying" any overflow from bit to bit as the addition proceeds. The algorithm to add register j to register i, leaving the result in register i, which will be written "Add i j", is then as follows.
Add i j Set the carry, c, to 0 Move to the least significant end of register i Leave a mark Move to the least significant end of register j (*) Read the bit, b Leave a mark Find the mark left in register i Add b and c to the bit, find new value of c Move the mark to the next bit Find the mark left in register j Erase the mark Move to the next bit Goto (*) if there are any bits left
As mentioned in the discussion of the "Mov" instruction, the values of b and c must be remembered by duplicating the appropriate sections of the state table, and so in this case certain sections will appear four times, once for each of the possible combinations of values of b and c. Also, the details of the marks left will vary depending on whether i < j or i > j. Note that there is no need to be able to add a register to itself (the excluded case i = j) as this can be accomplished, should it be necessary, by shifting the register left.
The actual algorithm in terms of state tables can be found in Appendix B as it is rather too long to present in full here.
Before considering the algorithm which will be used to multiply two registers together, we must consider how to negate a register, ie. replace the value of a register with its negative. This must be done as multiplication of binary integers which are stored in the two's complement system described above cannot be multiplied directly; for example in a four-bit system, -1 is stored as 1111, -2 as 1110, and 1111 multiplied by 1110 is 11010010, which represents -46. Therefore, negative numbers must be converted to positive ones before the multiplication, and then the result negated if exactly one of the multiplicands was negative.
It is easy to see that in the two's complement system, the negative of a number can be obtained by first inverting the register, i.e., changing all the 1s to 0s and vice versa, and then adding one to the result. Inversion of a register is quite simple to achieve, being basically the algorithm for zeroing a register with only the line which acts on the actual bits being altered. The following code implements an instruction, which will be written "Not i", for inverting the contents of register i.
Not i FindReg i L "0 0 0 L 1; 0 1 1 R 3" "0 0 1 L 1; 0 1 0 L 1" "0 0 0 L -3; 0 1 1 L -3" FindStart
We can avoid having to use the long adding routine above to increment a register by noticing that, working leftwards from the least significant end, this can be effected by changing 1s to 0s until the first 0 is encountered; this 0 is then changed to a 1 and the procedure is complete. If no 0 is encountered before the end of the register, then this algorithm will turn 11...11 into 00...00, the correct result. The instruction "Inc i", which increments register i, can be coded as a state table as follows.
Inc i FindReg i L "0 0 0 L 1; 0 1 1 R 3" "0 0 1 L 2; 0 1 0 L 1" "0 0 0 L -3; 0 1 1 L -3" FindStart
Concatenating these two instructions would give an algorithm for negating a register ("Not i, Inc i"), but this would involve unnecessary moving backwards and forwards along the tape, and so instead we combine them at a more basic level. By considering the effect of each operation on the bits, we see that negation can be effected by working leftwards from the least significant end of the register until the first 1 is encountered. All bits to the left of this 1 are then inverted. If no 1 is encountered, the register, which must hold 00...00, is unaltered; this is the correct result since -0 = 0. The state table coding of this is
Neg i FindReg i L "0 0 0 L 1; 0 1 1 R 7" "0 0 0 L 1; 0 1 1 L 5" "0 0 0 L -3; 0 1 1 L -3" L "0 0 0 L 1; 0 1 1 R 3" "0 0 1 L 1; 0 1 0 L 1" "0 0 0 L -3; 0 1 1 L -3" FindStart
which is much more compact than simply concatenating the two state tables given above.
A few times in the algorithm it will prove necessary to perform some operation a set number of times; for example the basic decision algorithm must be executed 40 times per row of the sample grid, and the multiplication routine must include code to shift the result right 15 times as mentioned in the discussion concerning the representation of real numbers. Therefore, we will write code for an instruction "Loop i d", which, given a register number, i, and a destination state, d, performs the following.
Decrease register i If register i is now non-zero then go to state d If register i is now zero, fall through to the next instruction
Then the example given concerning the multiplication routine would be coded as
Load register x with 15 :SHIFT: Shift product right Loop x :SHIFT:
where x is some register number not used for any other purpose. By adapting the algorithm given above for incrementing a register, we see that to decrement a register we work from the least significant end, changing 0s to 1s until the first 1 is reached; this 1 is then changed to a 0 and the process terminates. Also, the decremented register can only be zero if the first bit was a 1 and the remainder 0s. Therefore, by combining the decrement algorithm with this test, we see that "Loop i d" can be coded as follows.
Loop i d FindReg i L2 "0 0 1 L 1; 0 1 0 L :L1:" If the first bit was 1, reg. i could now be zero :L0: L2 "0 0 0 L 1; 0 1 1 R :L2:" "0 0 1 L :L0:; 0 1 0 L :L2:" :L1: Check whether the register is now zero L2 Move to delimiter "0 0 0 L 1; 0 1 1 R :L2:" If it is 1, the reg. is zero -- fall through "0 0 0 L :L1:; 0 1 1 L 1" If the bit is 1, the reg. is not zero -- go to d FindStart Goto d :L2: FindStart
Multiplication of registers could be achieved by repeated addition, but even by applying some common sense and choosing the higher register to be repeatedly added, this method would still take time O(min(x, y)), where x and y are the values of the registers to be multiplied, and it assumed that the most time-consuming part of the operation is the addition (rather than the counting of number of additions completed, looping instructions, etc.). Since our values of x and y will be of the order of tens of thousands (recall that, for example, 1.7 is stored as 1.7 * 215 = 55706), this method is not likely to be astoundingly efficient.
Instead, we adapt the method of long multiplication used to perform larger multiplications with pen and paper in the decimal system. To start with, we deal with the case when the two registers to be multiplied are both positive. Two 40-bit working registers are required. The first of this is zeroed at the start of the algorithm; it will hold the product as it is built up by addition, and will be called the cumulative sum register. The second is initialised with one of the multiplicands. If the least significant bit of the other multiplicand is 1, this second working register is added into the cumulative sum register (this effects multiplication by this bit since it can only contain 0 or 1). The second working register is then shifted left. The second least significant bit of the second multiplicand is tested; if it is 1, the second working register is added into the cumulative sum register. This continues until all bits of the second multiplicand have been tested and the second working register has thus been shifted 20 times (for our registers of 20 bits' length). As a pseudo-code algorithm this is as follows, writing WRi for working register i.
Zero WR1 Copy register i into WR2 If bottom bit of register j is 1, add WR2 into WR1 (*) Shift WR2 left If next bit of register j is 1, add WR2 into WR1 If end of register j has not been reached, go to (*)
It is easy to verify that this does multiply the two registers as required. To take account of the fact that the registers may contain negative numbers, we introduce a "sign flag". This is a one-bit register which is initially zero; it is then incremented once for each negative multiplicand. At the same time, if a multiplicand is negative, that multiplicand is negated. Thus, since for a one-bit register adding 1 to 1 gives 0, the sign flag will hold 1 iff exactly one multiplicand was negative, and both multiplicands will now be positive. Therefore, after the multiplication, if the sign flag holds 1 we must negate the result.
We also need, as noted in the discussion concerning the multiplication of real numbers held in fixed point format, to shift the result right 15 places and so require a further register to hold the shift counter. By a stroke of good fortune, 15 in binary is 1111, so we may initialise this (four-bit) register by first zeroing then inverting it.
As multiplication will be used many times in the Mandelbrot algorithm, we place the working registers (including the sign flag and the shift counter) at the start of the register section of the tape, where they can be located more quickly than if other registers were placed before them. Therefore, the registers given below are reserved for use by the multiplication routine alone.
| Register number | Description | Length (bits) |
|---|---|---|
| 1 | Sign flag | 1 |
| 2 | Cumulative sum | 40 |
| 3 | Shifted multiplicand | 40 |
| 4 | Other multiplicand | 20 |
| 5 | Shift counter | 4 |
The instruction "Mul i j" is therefore given by the algorithm below, which gives execution times of O(Lg x) where Lg denotes logarithm to the base two, and x is the second multiplicand (the contents of register j).
Mul i j Zero registers 1, 2 and 5 Invert register 5 Move with sign extend register i into register 3 Move register j into register 4 If register 3 is negative, then negate register 3 and increment register 1 If register 4 is negative, then negate register 4 and increment register 1 If bottom bit of register 4 is 1, then add register 3 into register 2 (*) Shift register 3 left If next bit of register 4 is 1, then add register 3 into register 2 If end of register 4 has not been reached, go to (*) If register 1 holds 1 then negate register 2 (**) Arithmetically shift register 2 right Decrement register 5; if non-zero then goto (**) Move with sign de-extend register 2 into register i
This algorithm in state table form is presented in Appendix C since, again, it is rather too long to present in full here.
In the algorithm for the Mandelbrot plot, at each iteration we must determine whether the modulus squared of fn(c) has exceeded four (this is easier than comparing |fn(c)| with 2 since we avoid having to extract the square root of a number, a time-consuming task), and if it has we conclude that c is not in M. Therefore, we must be able to compare two registers and act differently depending on which is larger. This can be achieved by subtracting one from the other and then comparing the result with zero. In the two's complement system, this is easily done by examining the top bit; if it is 1, the number represented is negative, if 0, it is positive or zero. Therefore, we code an "jump if positive" instruction "JPos i d" which examines the contents of register i, and jumps to state d iff they are positive or zero; otherwise execution proceeds with the next instruction. The algorithm is as follows.
JPos i d FindSReg i Move to the significant end of register i R2 Move to the top bit "0 0 0 L 1; 0 1 1 L :L0:" Decide whether the register is non-negative FindStart It is -- return to home position Goto d and go to state d :L0: FindStart The register is negative -- fall through
When the algorithm has decided whether the point sampled lies inside or outside the Mandelbrot set, the corresponding result bit (0 for inside, 1 for outside) must be appended to the output section of the tape in the format described under "output format" above. The instruction to achieve this will be written "Out b", where b is 0 or 1, and the state-table coding is as given below.
The coding for "Out 0" is
Out 0 Lto 2 1 Find end of output delimiter R2 Move to where 0 will go Write 0 and write it L Write 1 Replace the 11 delimiter L Write 1 Rto 3 1 Return to the home position L3
The coding for "Out 1" is
Out 1 Lto 2 1 Find end of output delimiter R2 Move to where 1 will go Write 1 and write it L Write 0 L Write 1 Replace the 11 delimiter L Write 1 Rto 3 1 Return to the home position L3
Now that we have coded as state tables the individual elements which are to make up the Mandelbrot algorithm, we can present the algorithm itself in terms of these elements. Instead of register numbers, symbols have been used to make clearer the intention of each instruction. Note that the current value of fn(c) has been denoted z, and that the iteration counter has been initialised to 15 by zeroing then inverting it, a trick used in the shifting section of the multiplication routine.
:Do_A_Row: Mov CRe CRe0 Mov Cols Cols0 :Do_A_Pel: Clr ZRe Clr ZIm Clr Iters Not Iters :Iterate: Mov X ZRe Mul X ZRe Mov Y ZIm Mul Y ZIm Mov Mod X Add Mod Y Add Mod M_Four JPos Mod :NotInSet: Mul ZIm ZRe Shl ZIm Add ZIm CIm Mov ZRe X Neg Y Add ZRe Y Add ZRe CRe Loop Iters :Iterate: Out 0 Goto :Next_Pel :Not_In_Set: Out 1 :Next_Pel: Add CRe DCRe Loop Cols :Do_A_Pel: Add CIm DCIm Loop Rows :Do_A_Row:
The register numbers which the symbols ZRe, etc. stand for are given in the table below, which also includes the working registers used by the multiplication routine. Note that in the "initial value" column, parentheses surrounding a number x indicate that x is real and is stored in the fixed point notation described above. Numbers without parentheses are stored as their binary integer representations. Registers with no initial value given are "don't care".
| Register number | Symbol | Description | Length (bits) | Initial value |
|---|---|---|---|---|
| 1 | - | Sign flag | 1 | - |
| 2 | - | Cumulative sum | 40 | - |
| 3 | - | Shifted multiplicand | 40 | - |
| 4 | - | Other multiplicand | 20 | - |
| 5 | - | Shift counter | 4 | - |
| 6 | ZRe | Real part of z | 20 | - |
| 7 | ZIm | Imag. part of z | 20 | - |
| 8 | Y | ZIm2 | 20 | - |
| 9 | X | ZRe2 | 20 | - |
| 10 | Mod | |z|2 | 20 | - |
| 11 | Iters | Iteration counter | 4 | - |
| 12 | CRe | Real part of c | 20 | - |
| 13 | CIm | Imag. part of c | 20 | (-1.45) |
| 14 | M_Four | Constant -4 | 20 | (-4) |
| 15 | DCRe | Increment in CRe | 20 | (0.1) |
| 16 | Cols | Column counter | 6 | - |
| 17 | DCIm | Increment in CIm | 20 | (0.1) |
| 18 | Rows | Row counter | 4 | 15 |
| 19 | CRe0 | Init. val. of CRe | 20 | (-2.45) |
| 20 | Cols0 | Init. val. of Cols | 6 | 40 |
A compiler was written in BASIC on a 486-based PC to produce a state table from the algorithm given above, and this resulted in a state table of roughly 5,200 states. (The state table is not given here.) The input tape was set up with the delimiters and initial register values where necessary. A Turing machine simulator capable of executing roughly 37,000 Turing machine cycles per second was written in 8086-family assembly language (to produce this running speed). The source code for these programs is given in Appendices D and E.
The simulator was run with the state table produced by the compiler, and the resulting tape was decoded to give the plot shown in the figure below. A point that was given by the algorithm to be in the set is represented by a filled square, one not in the set by blank space. The simulation took 2,097,543,785 cycles of the Turing machine; nearly 16 hours of real time. Note that the results given on the final tape have been reflected in the imaginary axis to give the complete figure, since the Mandelbrot set is symmetrical about this axis as noted in the introduction to the problem.
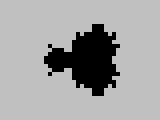
This image is just about recognisable as being of the Mandelbrot set; its resolution is not wonderful, but one can make out the main cardioid "body" and the circular "buds" to its left and, with some imagination, to its top and bottom.
The Turing machine was originally intended to be a starting point from which the study of computability could be developed. Therefore, we might hope that a suitably programmed Turing machine could perform any task that a real-world computer can; in fact strictly more tasks than a real-world computer, for the Turing machine is a potentially infinite device, whereas real-world computers are necessarily finite.
In this essay we have examined how a Turing machine can be programmed to perform one such useful computational task; that of plotting an image of the Mandelbrot set. This task is not one for which a state table immediately springs to mind, and so the final table was built from successively more complicated elements. This method of building up complex Turing machines from simpler elements mirrors the theoretical development of computability in which successively more complex functions are shown to be (Turing-) computable.
The state table produced is doubtless not the most efficient one giving the required results, but it does have the advantage that its gradual development was fairly painless. By expanding these methods and ideas more thoroughly, we could obtain some evidence for the Church- Turing thesis, among the implications of which is that any task which we think ought, informally and intuitively, to be computable can be performed (albeit perhaps very slowly) by a suitably programmed Turing machine.
Ben North
September, 1993.
The state tables referred to in the text as too long to be presented in full there are given here. However, in the interests of efficiency some slight optimisations have been made in the translation, particularly in the decision-making instructions. Therefore, some differences may be encountered.
Brief comments are given to the right of the actual algorithm lines.
Brief comments are written to the right of the actual algorithms.
The algorithm coding the instruction "Mul i j" is as follows; brief comments are given to the right of the instructions.
Here we present the assembly language source code for the Turing machine simulator which was used in the development and running of the Mandelbrot set plotting algorithm. The assembler used was Eric Isaacson's A86/D86 assembler/debugger package. The code is split up into chunks based on the function of the following procedures. Again, no explanation of the operation of the simulator is given here; there should be sufficient comments in the code to allow the reader reasonably conversant with 8086-family assembly language and the PC's internal organisation to follow the operation. Appended to the source code is the documentation for the program.
Here we present the BASIC source code for the compiler which translates algorithms given in the form in Appendices A-C into a state table in the form required by the Turing simulator whose source code appears in Appendix D. The BASIC used was Microsoft's QBasic, supplied with its MSDOS operating system. Minimal comments are given within the source code. As it is not the purpose of this essay to discuss compiler design, the program and its operation are left largely unexplained.
Note that some of the algorithms which the compiler produces have been subjected to slight optimisations. For example, sequences such as "Write 0, L" are coded as "0 0 0 L 1; 0 1 0 L 1" rather than the six lines "0 0 0 L 1; 0 1 0 L 1; 1 0 0 R 2; 1 1 1 R 2; 2 0 0 L 3; 2 1 1 L 3" which a strict compilation would give. Therefore, there will be some differences between the state tables produced by the compiler and those presented in the text and Appendices A-C, and also a few extra instructions, including the "w0L" example given above.
After digging out the above essay and image, I re-wrote the Turing simulator in C on a GNU/Linux system based on an Athlon running at 1.667GHz, and re-ran the Turing machine above. This took about 75 seconds; when compared to the original 16 hours, this is a speed-up of around 750 times. (Processors have come a long way.) I made some changes to the initial tape, to produce a higher-resolution image, and after 30,216,448,648 cycles (about half an hour of simulation), decoded the tape to get:

This is a much better image, but the framing could be improved. One more set of adjustments to the parameters gave:

which took 48,319,931,608 cycles and 45 minutes. There may well be some artifacts emerging because of the limits of the fixed-point arithmetic used, or it may just be that the limited resolution is causing the lumpiness of this image.
(Address as image to foil spam-harvesters, sorry.) Or see other things on redfrontdoor.
![]()