Guess Poo: An application of nearly-orthogonal fractional factorial design

We have the game ‘Guess Who’, which comes with a selection of sheets to play variants of the original game. In a flash of comedy inspiration, my eldest, Marlowe, and I thought it would be excellent if there was a game called ‘Guess Poo‘. In Guess Poo, instead of trying to identify faces, you have to identify faeces.
We therefore set about designing drop-in sheets for our game.
(‘Guess Who’ is probably a trademark of Hasbro or Milton Bradley, and I would be very surprised indeed if either of them endorsed this post.)
Choice of characteristics
In the original, the faces have different values for various characteristics, such as hair colour, whether they wear glasses, gender, and so on. It didn’t take too long to come up with six qualities that the various poos could have: size, colour, number of flies, smelliness/steamingness, number of pieces, neatness of formation.
Each characteristic has two or three possibilities, and we have to choose 24 poos out of the 144 combinations. What is a good way to do this? What are we trying to achieve? We want to make sure that the characteristics are as independent as possible. The game would not be very good if, say, all the neatly-formed poos were also steaming.
An equivalent problem shows up in experimental design. Say you have nine factors which you think might affect the behaviour of a testing device for blood glucose: centrifuge speed, temperature, dilution ratio, and six others. We would like to know what effect these all have on the readings. To test every combination would be too expensive, so we want to choose a subset of the possibilities in such a way that we get the most information about each factor by itself, and also about the interactions between different factors. The full set of combinations is a ‘full factorial’ design; if you only do some of them, it’s a ‘fractional factorial’ design; and a design with the independence property we seek (which we might not be able to fully achieve) is called ‘orthogonal’. So we’re looking for a nearly-orthogonal fractional factorial design.
Luckily, there is a body of research on this question, and I found a paper [Xu, 2002] with published source code for the algorithm it proposes. This paper also provided the blood glucose example above. I don’t know whether this paper is the current state of the art, but it looked sufficient for our purposes. Running the code gave the 24 poos used. Names of dogs were chosen by asking the internet for a list of popular dog names.
Implementation
Marlowe and I used Inkscape to create the required illustrations, with a fair bit of copy and paste. Some examples:
 |
 |
 |
Measuring an existing sheet of human Guess Who characters allowed me to put the whole thing together. The sheets are available in the Downloads section below.
It fits pretty well in the game:

Sample game
This is how one real game evolved, as played by two of my other children:
| Sally | Jude |
|---|---|
| Is it in two bits? | |
| Yes. Does yours have any flies? | |
| Yes it does. Is yours light in colour? | |
| Yes. Is yours sloppy? | |
| No, neatly formed. Is yours little? | |
| Yup. Is yours smelly (at all)? | |
| No. Is yours sloppy? | |
| Yes. Is yours small? | |
| Yeah. Is yours Ziggy? | |
| No. Is yours Angel? | |
| No. Is yours Gizmo? | |
| Yes. Yours is Fluffy. | |
| Yes. | |
Here you can see that incisive questioning led Sally to victory, but Jude was only one move behind. You can follow along on the sheets (below) and check their analyses.
Downloads
As in the original, the two players have the smaller rows at the top arranged differently. The lower section, where you flip over the covers is the same, though.
The ‘padded to 8×12’ versions are ready for photo-printing onto 8×12-inch paper, which is what I did.
All downloads here are available under the Creative Commons ‘Attribution-ShareAlike’ licence.
| Player 1 | Player 2 |
|---|---|
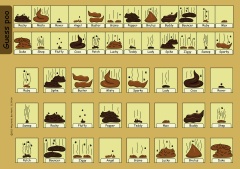 |
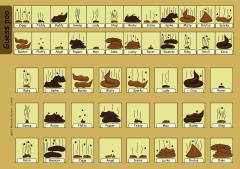 |
| [PDF] | [PDF] |
| [JPG] | [JPG] |
| [JPG padded to 8×12] | [JPG padded to 8×12] |
Assessment and future work
Having actually played a few games, I think the near-perfect balance between the poos having different values of the same characteristic makes the game less good than the original. In the original, you usually cannot cut the remaining possibilities in half each time, and this makes the game more interesting. The three-way split of flies and smelliness works better than the half-and-half split of size, colour, neatly-formed-ness, and number of pieces. No doubt one could modify the selection algorithm to give a non-balanced distribution over the levels, and bringing in some correlation between factors might help game-play too.
It was good to find a setting where Comic Sans is a suitable choice of font.
There are other games which could benefit from this treatment. One could imagine a variant on Cluedo called Poo-do. ‘I suspect Colonel Ketchup in the downstairs toilet after a dodgy onion bhaji’. I haven’t worked out how Mono-poo-ly could work but surely there’s potential there.